algebraaritmetica81

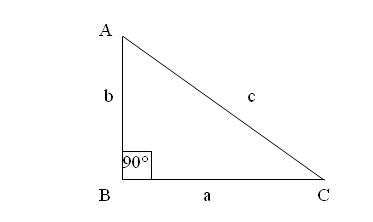
FUNCIONES TRIGONOMÉTRICAS

Para las Funciones Trigonométricas, como se mencionó anteriormente,

haremos uso del Teorema de Pitágoras y trabajaremos con las Funciones

de Seno, Coseno y Tangente, y sus inversas, además de apoyarnos

siempre con la Calculadora.
Las letras minúsculas son las que utilizamos en el Teorema de Pitágoras,

las letras Mayúsculas, en éste caso, se utilizarán para referirnos a los

Ángulos del Triángulo.

Empezaremos a ver cada una de las Funciones:
1. Función  Seno ( Sen):
    
    La Función Seno nos describe la relación  existente entre Lado Opuesto sobre la
    
    Hipotenusa. Su simbología es la siguiente:
 
                  
2. Función Coseno ( Cos):

La Función Coseno describe la relación entre Lado Adyacente sobre

Hipotenusa. Su simbología es la siguiente:
             
3. Función Tangente ( Tan):

Ésta Función nos representa la relación entre Lado Adyacente sobre

Hipotenusa. Su simbología es la siguiente:

       También tenemos las  Funciones que son inversas a las anteriores:

       4.  Función  Cotangente ( Cot):
            
            Que describe la relación  entre Lado Adyacente con Lado Opuesto:

       5.  Función Secante (  Sec):
            
            Relación entre Hipotenusa sobre  Lado Adyacente:

       6.  Función  Cosecante ( CsC):

            Nos muestra la relación entre Hipotenusa  sobre  Lado Opuesto:

ARITMETICA

RAZONES Y PROPORCIONES

Denominamos razón al cociente que es indicado por dos números y una proporción a la igualdad que existe entre dos o más razones. Estudiemos algunos ejemplos de razones y ejemplos de proporciones para clarificar mejor estas nociones matemáticas.

Ejemplo de Razones

En una clase de un colegio cada pelota es utilizada por cada cinco niños, o sea que tenemos cinco veces más alumnos que pelotas de fútbol. Tenemos entonces en este ejemplo de razón que la relación entre alumnos – pelotas es 5 a 1. Esta razón se denota 5/1 y la podemos leer como: cinco es a uno. El valor de la razón la obtenemos dividiendo 5/1=5. Concluimos con este ejemplo de razón que existe el quíntuple de alumnos que de pelotas de fútbol.

Ejemplo de Proporciones

Continuando con el ejemplo anterior, si las pelotas son 7, ¿cuántos son los alumnos? Del ejemplo anterior de rezones sabemos que hay 5 alumnos por cada pelota de fútbol: 5/1. Entonces, si ahora tenemos siete pelotas significa que la cantidad de alumnos es de 35.

5 ------ 35
1 ------- 7

La cantidad de balones de fútbol y alumnos guardan una relación que es proporcional. En este ejemplo las

dos razones son proporcionales:

5/1 = 35/7

En todas las proporciones, el producto de los medios es igual al producto de los extremos:

Producto de los medios: 1 x 35 = 35

Producto de los extremos: 5 x 7 = 35

Para leerlo expresamos que 5 es a 1 como 35 es a 7.

Ejemplos de razones y su valor:
1-      40/20 = 2 y se lee cuarenta es a veinte
2-      12/8 = 1,5 y se lee doce es a ocho
3-      8/2 = 4 y se lee ocho es a dos
4-      9/3 = 3 y se lee nueve es a tres
5-      24/6 = 4 y se lee veinticuatro es a seis

Más ejemplos de razones proporcionales: